Differentiable Optics &
∂Lux
Louis DesdoigtsThe University of Sydney
louisdesdoigts.github.io/diff_optics/
Code and examples available
Benjamin Pope (UQ)
Peter Tuthill (USyd)
Jordan Dennis, student (UQ)
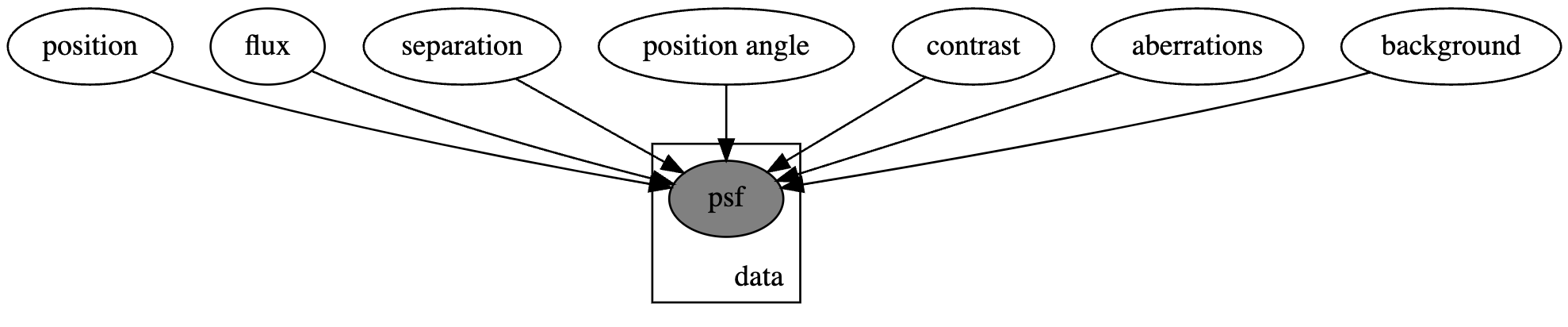
Inference & Design Problems in Optics
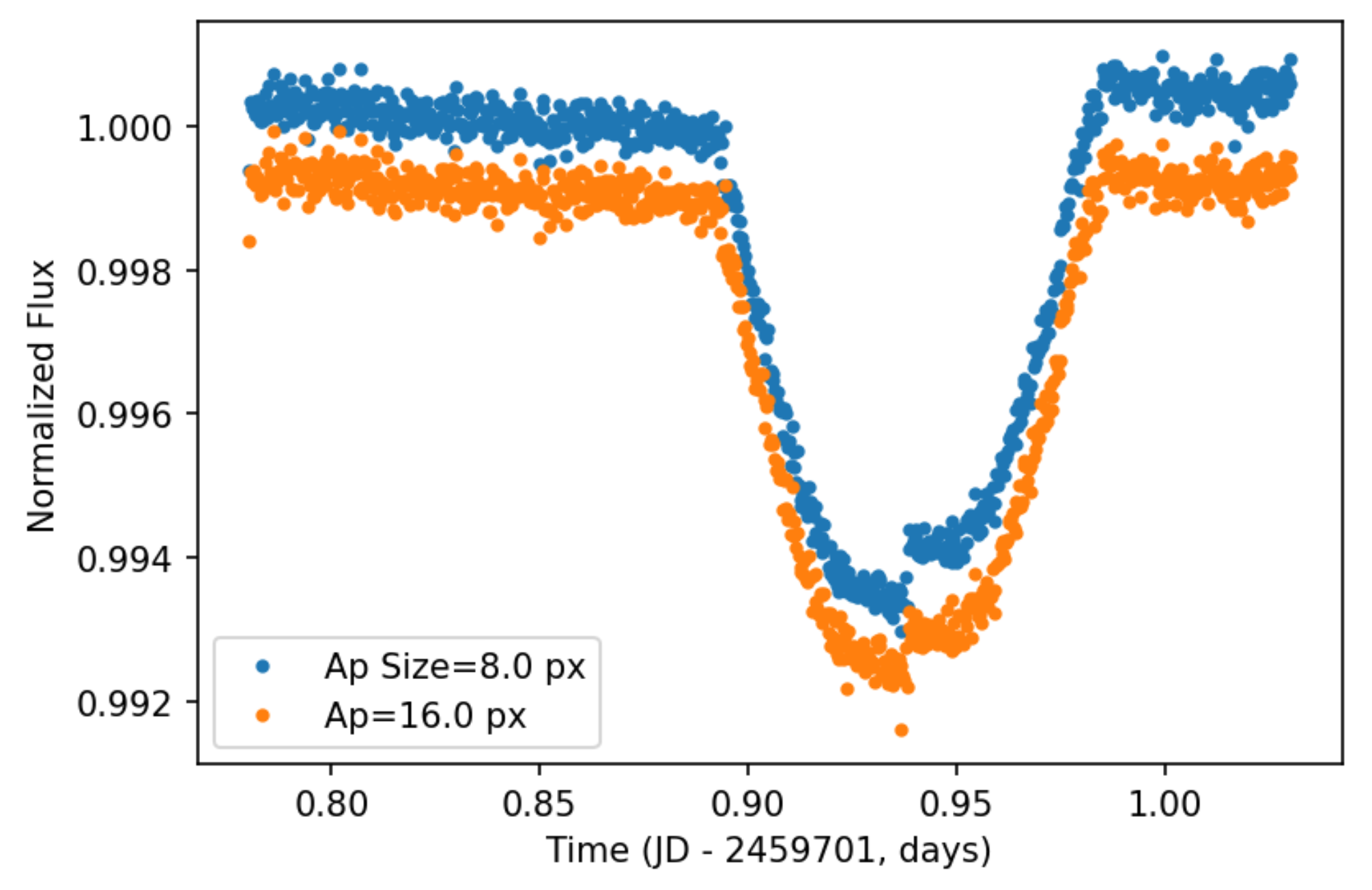
JWST, Toliman, & Beyond!Phase Retireval
Instrumental Calibration
Toliman
μ-arcsecond astrometry
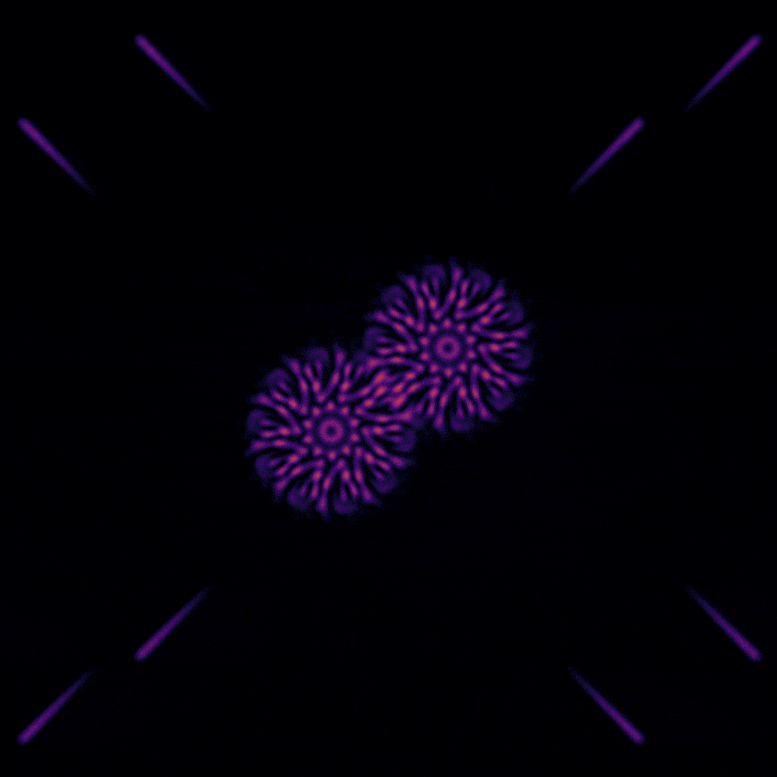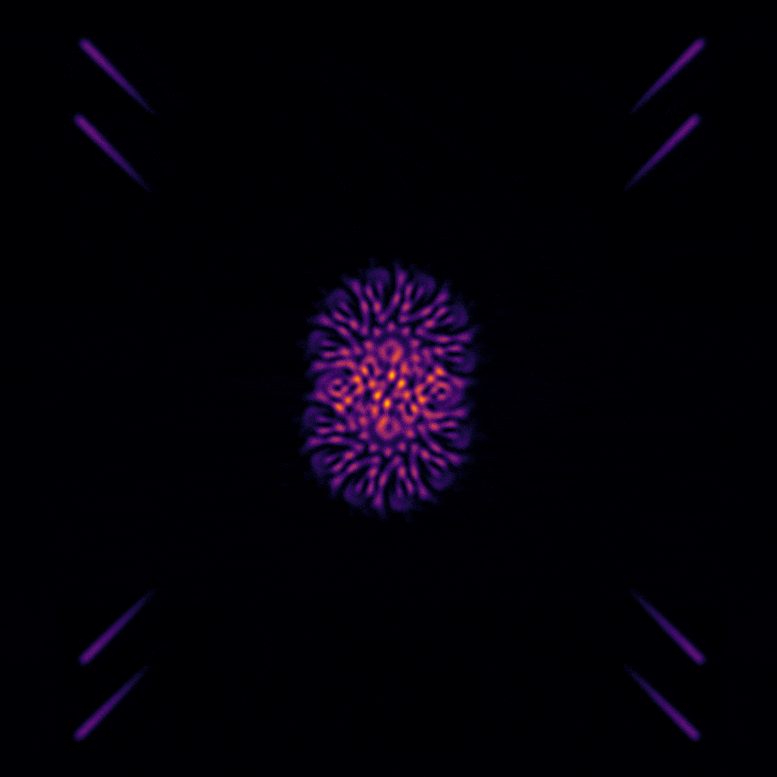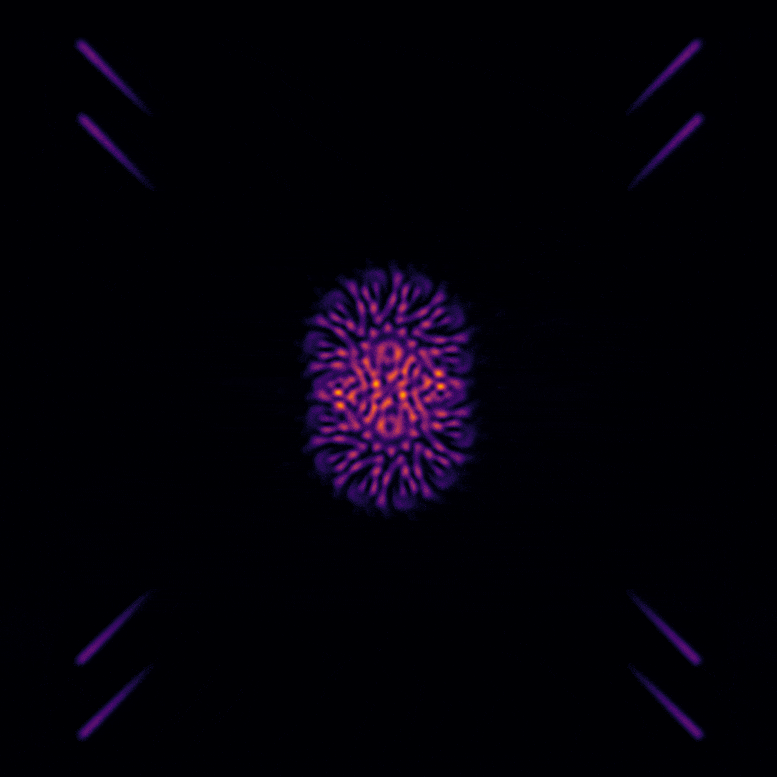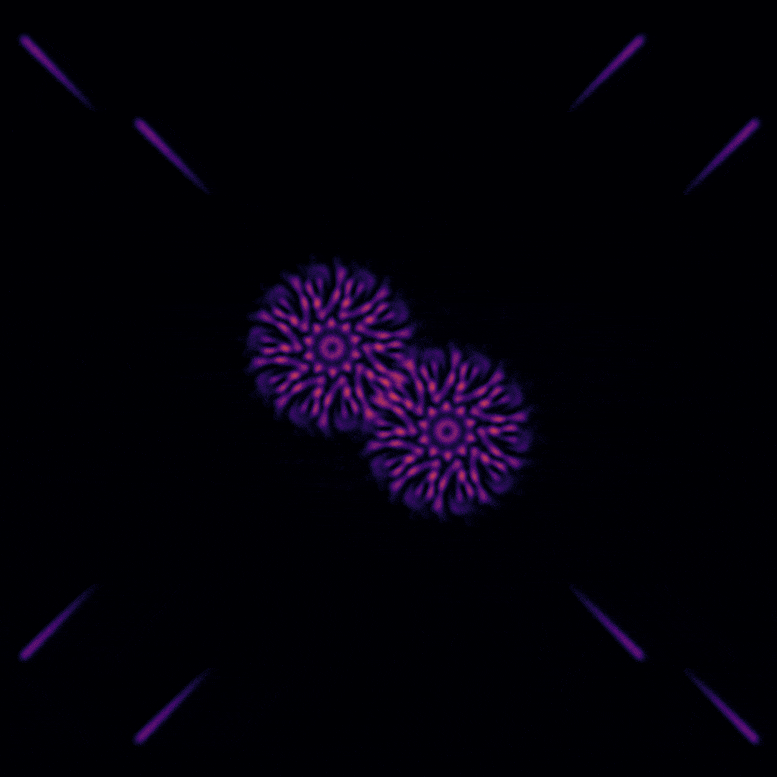
Beyond!
Low-order wavefront error resistant coronagraphs
Polarisation invariant coatings
Non-common path error correction in AO
Crowded-field signal decontamination
*Your science goes here!*
Automatic Differentiation & Optics
Unifying Machine Learning and OpticsIsomorphism
What does a Neural Network DO?
Isomorphism
What does an Optical System DO?
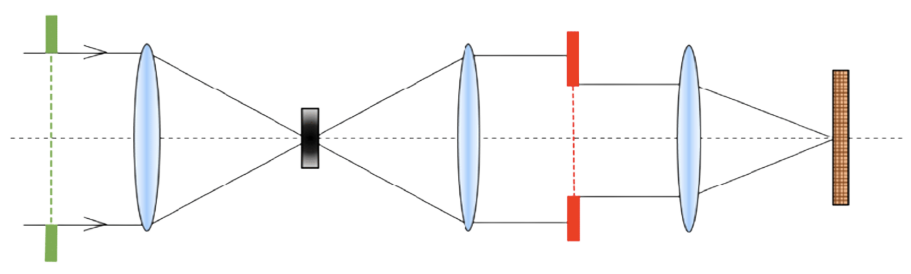
Neural Network and Optical Systems are structurally isomorphic
Optical forwards models constructed within ML frameworks can harness Automatic Differentiation!
Automatic Differentiation
What is Autodiff?
- It is NOT finite differencing
- It is NOT symbolic differentiation
- It IS repeated applications of the chain rule to code in order to calcualte derivates
Automatic Differentiation
Why is autodiff usefull?
- Computational cost of derivative calcualtions do Not scale with the number of parameters
- Complex, high-dimensional models can optimised simply
- Parameter gradients let us access a host of better optimsation and inference algorithms!
∂Lux - An open source, Python based, fully differentiable optical modelling framework using Google Jax & Equinox
∂Lux
Toliman Diffractive Pupil Design
How can you design a binary mask using gradients?
Continuous Latent Image Mask Binarisation
(CLIMB)
CLIMB
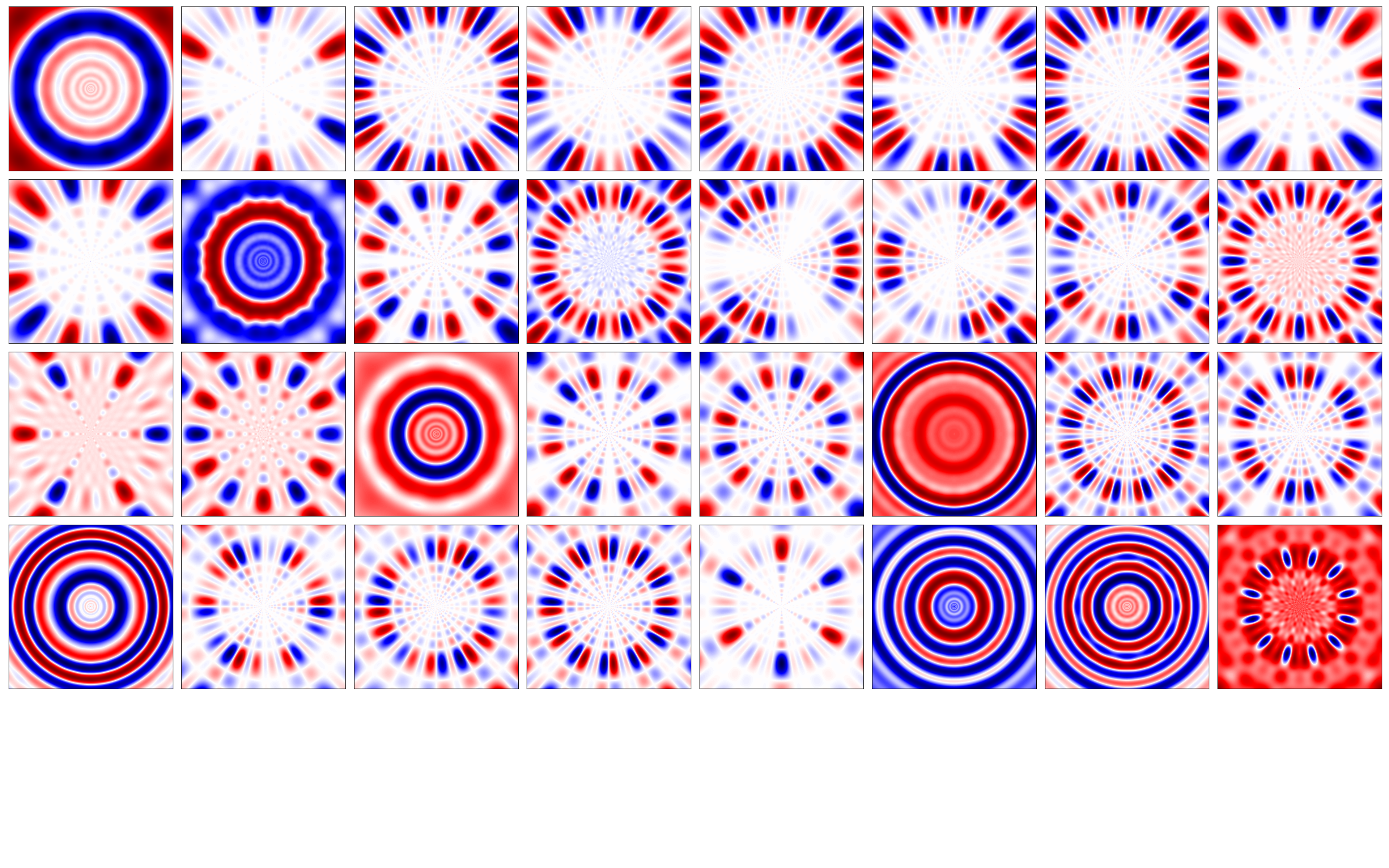
CLIMB
How do you design a mask to best constrain binary-star separation AND the instantaneous state of the telescope?
Engineer a loss function!
\[ \text{Loss}(\psi, p) = - \sum_{(x, y)} \Big(\nabla \psi(x, y) (\alpha + \beta\vec{r})\Big)^p \]Optical Design
Cramer-Rao lower-bound calcualtion under the Laplace approximation
\[ \text{CRLB}(\vec{X}) \propto \frac{1}{\vec{\Sigma}(\vec{X})} \] where \[ \vec{\Sigma}(\vec{X}) = - \Big[ \nabla \nabla \text{ln} \Big( \mathcal {L}(\vec{X}) \rho(\vec{X}) \Big) \Big]^{-1} \]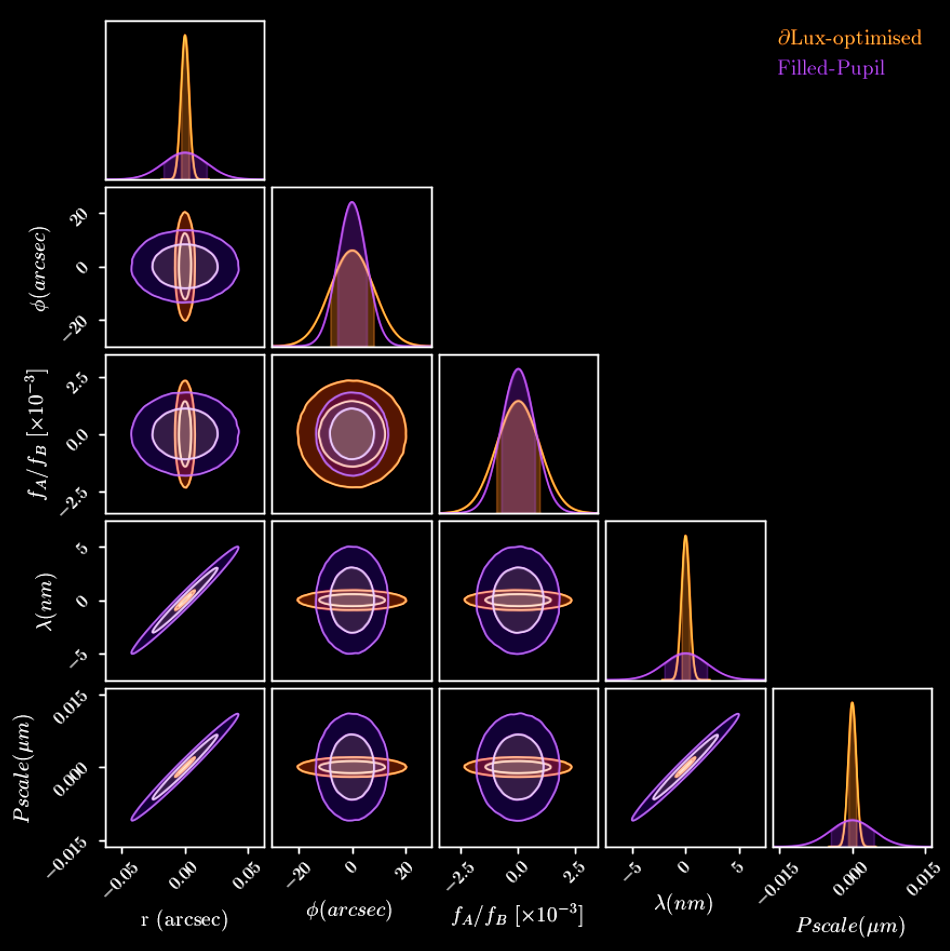
Going further...
What if we optimised the entropy of the covariance matrix?
Data Analysis
How to understand relationships between a large number of interrelated parameters from data?
Hamiltonian Monte Carlo (HMC)
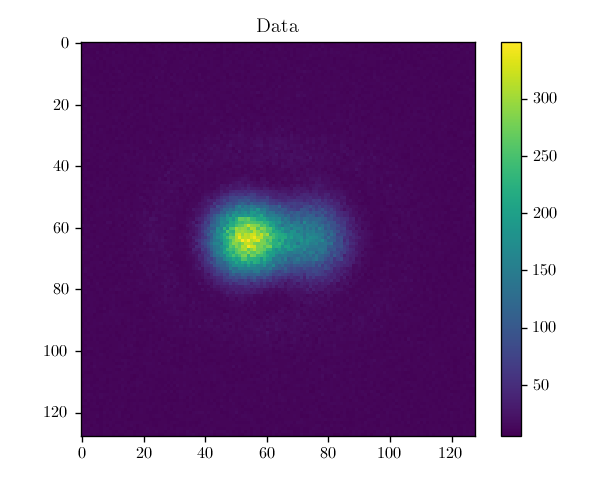
Phase Retrieval & Instrumental Calibration
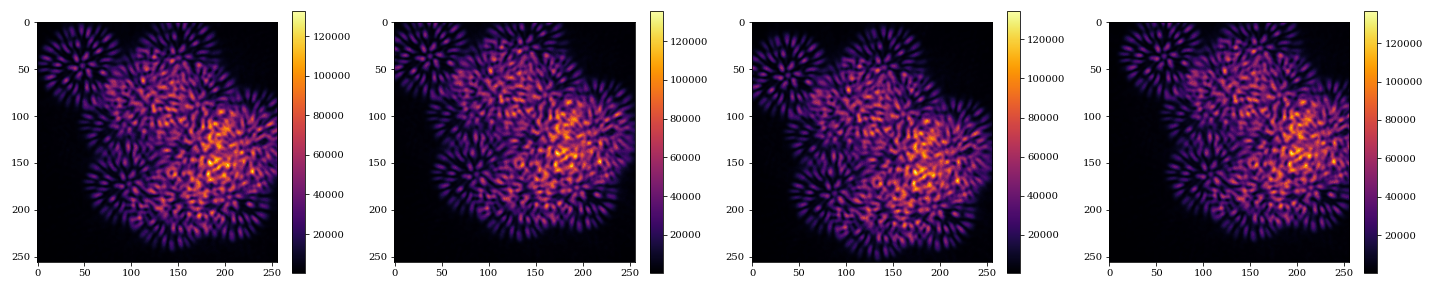Initial Resdiuals
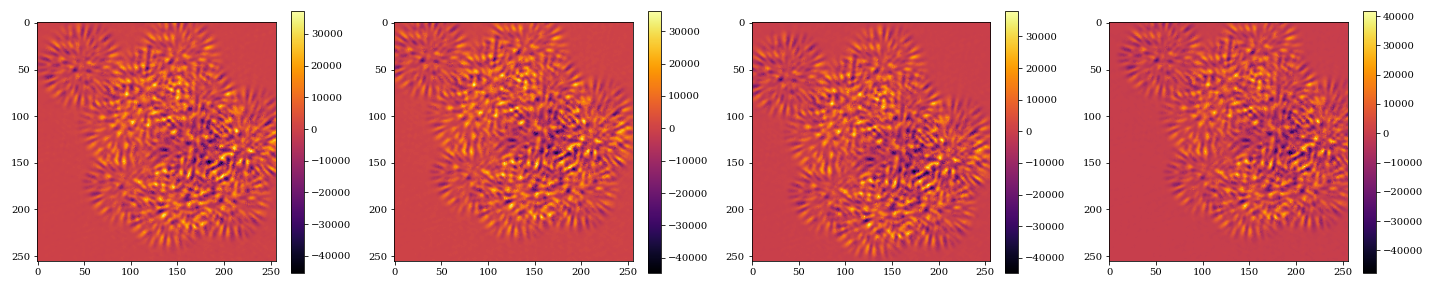
Run gradient descent on:
- Stellar positions & fluxes (45 parameters)
- Optical aberrations (11 parameters)
- Interpixel sensitivites (65'536 parameters)
Astrophysical parameter recovery
Optical aberration recovery
Inter-pixel sensitivity recovery
Future Work
Bulk optic design with ray tracing
Holographic phase mask design
Non-common path error correction using physical forwards models
Your optical problems!